Assalamu'alaikum warahmatullahi wabarakatuh,
Nama : Nadila Danti Lestari
NIM : 202031038
Kelas : B
Dosen pembimbing : Ibu Efy Yosrita S.Si., M.Kom.
Fakultas Telematika Energi
Program Studi. : Teknik Informatika
Apa itu kalkulus? buat apa sih belajar kalkulus? Sulit ga sih?
Kalkulus berasal dari bahasa latin yaitu calculus yang artinya "batu kecil", untuk menghitung. Jadi kalkulus adalah cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret tak terhingga. Kalkulus adalah ilmu yang mempelajari perubahan, sebagaimana geometri yang mempelajari bentuk dan aljabar yang mempelajari operasi dan penerapannya untuk memecahkan persamaan.
Kalkulus memiliki aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknik; serta dapat memecahkan berbagai masalah yang tidak dapat dipecahkan dengan aljabar elementer.
Jadi kalkulus itu tidak terlalu sulit, tapi kalau kita memiliki rasa ingin memahami dan tekun dalam belajar pasti kita akan lebih mudah dalam mengerti, begitu kata kakak tingkat yang pernah belajar mata kuliah kalkulus.
SISTEM BILANGAN (REAL)

Bilangan kompleks merupakan bilangan yang terdiri atas bilangan riil dan bilangan imajiner yang dilambangkan dengan a + ib. Dengan a dan b merupakan bilangan real.
Bilangan tersebut menjadi bilangan kompleks sebab keberadaan “i” atau dapat disebut sebagai bilangan imajiner. Pada bilangan kompleks berbentuk a+ib, bagian “a” merupakan bagian real, sedangkan “ib” merupakan bagian imajinernya.
Bilangan kompleks terbagi menjadi dua yaitu Bilangan riil dan bilangan imajiner :
1. Bilangan Imajiner (i)
Bilangan imajiner adalah bilangan yang didefinisikan dengan i² = -1, dengan i merupakan simbol angka imajiner. Bilangan i dalam bahasa inggris disebut juga imaginary number.
2. Bilangan Real (R)
Bilangan riil atau bilangan real adalah sistem bilangan yang dapat ditulis dalam bentuk desimal. Angka desimal adalah angka berbasis 10 yang dibentuk dari angka 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ahli matematika mendefinisikan notasi bilangan real sebagai simbol R.
Contoh : -2, 3, 0, 0,75
Bilangan real terbagi menjadi dua yaitu Bilangan Irrasional dan Rasional :
• Bilangan Irasional (I)
Bilangan irasional merupakan suatu bilangan real yang tidak dapat dinyatakan dalam bentuk pecahan a/b (a per b). Berbeda dari bilangan rasional, bilangan irasional merupakan bilangan dengan bentuk desimal yang tidak berhingga.
Contoh: √2, π, dan e
-Bilangan π = 3,14 atau π = 22/7 penggunaannya belum tepat karena nilai π yang sebenernya yaitu 3,141592653589793… .
-Bilangan eksponensial (e) merupakan konstanta dengan nilai 2,7182818…
• Bilangan Rasional (Q)
Bilangan rasional adalah sebuah bilangan yang dapat dinyatakan ke dalam bentuk sembarang pecahan a/b (a per b), dengan ketentuan seperti, a dan b adalah bilangan bulat di mana bilangan a melambangkan pembilang dan b merupakan penyebut bilangan rasional, dan juga b ≠ 0. Jika penyebut dari bilangan pecahan atau rasional ini bernilai 0, maka bilangan ini menjadi tidak terdefinisi.
Contoh : ¼, 5, 0,16, 20
Bilangan Rasional terbagi menjadi 2 yaitu :
-Bilangan Pecahan
Bilangan pecahan adalah bilangan rasional yang dapat ditulis dalam bentuk a/b (a per b) atau dengan kata lain mempunyai pembilang dan penyebut, yang dimana a dan b merupakan bilangan bulat, b tidak sama dengan nol, dan bilangan a bukan kelipatan bilangan b.
Bilangan pecahan terbagi menjadi 2 yaitu :
1. Pecahan berulang
Contoh : 0,66..... = 4/6
2. Pecahan berhenti
Contoh : 0,5 = ½
- Bilangan Bulat (Z)
Bilangan bulat adalah bilangan yang terdiri dari bilangan cacah dan negatifnya. Bilangan bulat dituliskan tanpa komponen desimal atau pecahan.
Contoh : -4, -3, -2, -1, 0, 1, 2, 3, 4
Bilangan bulat terbagi menjadi 2 yaitu :
1). Bilangan bulat negatif (-) merupakan bilangan yang terletak disebelah kiri angka nol (0) pada sebuah garis bilangan.
Contoh : -1, -2, -3, -4, -5, -6, -7, -8...dst.
2). Bilangan cacah (W)
Bilangan cacah adalah himpunan bagian dari bilangan bulat yang dimulai dari angka 0 dan dilanjutkan dengan bilangan bulat positif, yaitu {0, 1, 2, 3, 4, 5, 6...}.
Bilangan cacah terbagi menjadi dua yaitu :
-Bilangan Nol
-Bilangan asli merupakan bilangan yang terletak disebelah kanan angka nol pada sebuah garis bilangan.
Contoh : 1, 2, 3, 4, 5, 6, 7, 8....dst.
Bilangan asli terbagi menjadi 4 yaitu :
-)Bilangan komposit : bagian dari bilangan asli yang memiliki lebih dari 2 faktor, sehingga bilangan komposit dapat dibagi lagi oleh bilangan lain selain angka 1 dan bilangan itu sendiri.
Contoh : 4, 6, 8, 9
-) Bilangan prima : Bilangan prima adalah bilangan lebih dari 1 dan hanya bisa dibagi dengan angka 1 atau bilangan itu sendiri.
Contoh : 2, 3, 5, 7...
-) Bilangan genap : 2, 4, 6, 8...
-) Bilangan ganjil : 1, 3, 5, 7, 9...
Operasi Bilangan :
1) Hukum komutatif: x + y = y + x dan xy = yx.
2) Hukum asosiatif: x + (y + z) = (x + y) + z dan x(yz) = (xy)z.
3) Hukum distributif: x(y + z) = xy + xz.
4) Elemen-elemen identitas:
Terhadap penjumlahan: 0 sebab x + 0 = x.
Terhadap perkalian: 1 sebab x.1 = x.
5) Invers (balikan): Setiap bilangan real x mempunyai invers aditif (disebut juga negatif) –x yangmemenuhi x + –x = 0 dan setiap bilangan real x yang tidak nol mempunyai invers multiplikatif (disebut juga balikan) yaitu x−1 yang
memenuhi x. x−1 = 1.
Sifat-sifat yang ada pada bilangan riil
Sifat-sifat urutan:
1) Trikotomi yaitu jika x dan y elemen bilangan-bilangan riil maka berlaku sebagai berikut:
x < y atau x = y atau x > y
2) Ketransitifan yaitu jika :
x < y dan y < z maka x < z
3) Penambahan yaitu jika :
x < y ⇔ x + z < y + z
4) Perkalian yaitu :
Jika z positif maka x < y ⇔ xz < yz
Jika z negatif maka x < y ⇔ xz > yz
Rabu, 17 Maret 2021
Pertidaksamaan
dan
Nilai Mutlak
1. Pengertian Pertidaksamaan
Pertidaksamaan adalah kalimat terbuka yang menyatakan antara dua hal hubungan yang tidak memiliki kesamaan atau tidak sama dengan, serta memakai berbagai tanda seperti:
< (kurang dari)
≤ (kurang dari atau sama dengan
> (lebih dari)
≥ (lebih dari atau sama dengan)
2. Sifat-Sifat Pertidaksamaan
1. Tanda pertidaksamaan tidak berubah jika kedua ruas ditambah atau dikurangi dengan bilangan yang sama.
Jika a < b maka :
a + c < b + c
a – c < b – c
2. Tanda pertidaksamaan tidak berubah jika kedua ruas dikali atau dibagi dengan bilangan positif yang sama.
Jika a < b, dan c adalah bilangan positif, maka :
a.c < b.c
a/b < b/c
3. Tanda pertidaksamaan akan berubah jika kedua ruas pertidaksamaan dikali atau dibagi dengan bilangan negatif yang sama
Jika a < b, dan c adalah bilangan negatif, maka:
a.c > b.c
a/c > b/c
4. Tanda pertidaksamaan tidak berubah jika kedua ruas positif masing-masing dikuadratkan
Jika a < b; a dan b sama-sama positif, maka: a² < b²
3. Jenis-jenis pertidaksamaan
1). Pertidaksamaan linear
2). Pertidaksamaan Kuadrat
3). Pertidaksamaan Pangkat Tinggi
4). Pertidaksamaan Pecahan
5). Pertidaksamaan bentuk akar (Irrasional)
6). Persamaan Nilai Mutlak
Berikut adalah beberapa jenis dari pertidaksamaan :
1. Pertidaksamaan linear
Pertidaksamaan linear merupakan pertidaksamaan yang di mana salah satu atau kedua ruasnya mengandung bentuk linier di dalam x.
Pertidaksamaa terbagi menjadi dua yaitu :
a. Pertidaksamaan Linear Satu Variabel (PtLSV)
Pertidaksamaan linear satu variabel merupakan suatu kalimat terbuka yang hanya mempunyai satu variabel dan berderajat satu serta memuat hubungan (<,>, ≥ atau ≤ ).
Tahapan dalam penyelesaian pertidaksamaan linier satu variabel, diantaranya yaitu:
Sifat Pertidaksamaan Linear Satu Variabel dapat dilakukan dengan cara Subtitusi, mengurangkan, menjumlahkan, mengkali, ataupun membagi kedua ruas pertidaksamaan dengan bilangan yang sama.
Pertidaksamaan A < B ekuivalen dengan:
A + C < B + C
A – C < B – C
A x C < B x C, bila C > 0 untuk seluruh x
A x C > B x C, bila C < 0 untuk seluruh x
A/C < B/C, bila C > 0 untuk seluruh x
A/C > B/C, bila C < 0 untuk seluruh x
Perlu kalian catat, beberapa sifat di atas juga berlaku untuk lambang “>” atau “<”.
Contoh :
x + 6 ≥ 8
x + 6 – 6 ≥ 8 – 6
x ≥ 2
b. Pertidaksamaan Linear Dua Variabel (SPtLDV)
Pertidaksamaan Linear Dua Variabel (SPLDV) merupakan suatu kalimat terbuka matematika yang di dalamnya memuat dua variabel. Dengan masing-masing variabel berderajat satu serta dihubungkan dengan tanda ketidaksamaan (>, <, ≤, atau ≥).
Maka, bentuk dari pertidaksamaan linear bisa kita tuliskan seperti berikut ini:
ax + by > c
ax + by < c
ax + by ≥ c
ax + by ≤ c
Tahapan dalam penyelesaian pertidaksamaan linier dua variabel, diantaranya yaitu:
1). Ubahlah tanda ketidaksamaan dari pertidaksamaan menjadi tanda sama dengan (=), sehingga diperoleh persamaan linear dua variabel.
2). Lukis grafik/garis dari persamaan linear dua variabel tadi. Hal ini dapat dilakukan dengan menentukan titik potong sumbu x dan sumbu y dari persamaan atau menggunakan dua titik sembarang yang dilalui oleh garis. Garis akan membagi dua bidang kartesius.
3). Lakukan uji titik yang tidak dilalui oleh garis (substitusi nilai x dan y titik ke pertidaksamaan). Jika menghasilkan pernyataan yang benar, artinya daerah tersebut merupakan penyelesaiannya, namun apabila menghasilkan pernyataan salah maka bagian lainnya lah yang merupakan penyelesaiaanya.
Contoh :
Tentukan daerah penyelesaian dari pertidaksamaan linear dua variabel berikut
3x + y < 9
Grafik Penyelesaian :
(Garis putus-putus digunakan menunjukkan tanda ketidaksamaan < atau > dengan kata lain tanda ketidaksamaan tanpa sama dengan).
Uji titik (0, 0)
3(0) + 0 < 9
0 < 9 (benar)
Karena pernyataannya menjadi benar, maka (0, 0) termasuk penyelesaianya. Sehingga daerah yang memuat (0, 0) merupakan penyelesaianya. Dalam hal ini yang daerah bersih merupakan penyelesaian dari pertidaksamaan.
2. Pertidaksamaan Kuadrat
Pertidaksamaan kuadrat adalah bentuk “penghubung”antara ruas kanan dan kiri merupakan penggunaan tanda pertidaksamaan seperti kurang dari (<), kurang dari sama dengan (≤), lebih dari (>) serta lebih dari sama dengan (≥) dengan pangkat tertinggi adalah 2.
Tahapan dalam penyelesaian pertidaksamaan kuadrat, diantaranya yaitu:
1). Ruas kanan dibuat menjadi nol
2). Faktorkan
3). Menentukan titik uji
4). Menentukan tanda untuk masin-masing daerah penyelesain
5). Menentukan himpunan penyelesaian
• Tentukan harga nol, yaitu nilai variabel yang menyebabkan nilai faktor sama dengan nol.
1. Jika tanda pertidaksamaan ≥ atau ≤, maka harga nol ditandai dengan titik hitam •
2.Jika tanda pertidaksamaan > atau <, maka harga nol ditandai dengan titik putih °
• Tentukan tanda (+) atau (–) pada masing-masing interval di garis bilangan. Caranya adalah dengan memasukkan salah satu bilangan pada interval tersebut pada persamaan di ruas kiri.
•Tanda pada garis bilangan berselang-seling, kecuali jika ada batas rangkap (harga nol yang muncul 2 kali atau sebanyak bilangan genap untuk pertidaksamaan tingkat tinggi), batas rangkap tidak merubah tanda.
Cara menentukan himpunan penyelesaian :
- Jika tanda pertidaksamaan > 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (+).
- Jika tanda pertidaksamaan < 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (–).
Contoh :
3. Pertidaksamaan Pangkat Tinggi
Pertidaksamaan Pangkat Tinggi merupakan pertidaksamaan dengan derajat lebih dari dua.
bentuk dari “penghubung” antara ruas kanan dan kiri meliputi diantaranya yaitu: kurang dari (<), kurang dari sama dengan (≤), lebih dari (>) dan lebih dari sama dengan (≥).
Tahapan dalam penyelesaian pertidaksamaan pangkat tinggi, diantaranya yaitu:
1). Memindahkan seluruh suku ke dalam satu ruas, yaitu pindahkan pada ruas kiri sehingga tidak akan menyisakan suku atau bersisa nol pada ruas kanan.
2). Memfaktorkan bentuk tersebut ke dalam bentuk dengan derajat lebih rendah.
3). Buat garis bilangan dan tentukan Himpunan penyelesaiannya.
Contoh :
4. Pertidaksamaan Pecahan
Pertidaksamaan pecahan adalah pertidaksamaan yang terdiri dari pembilang dan penyebut, pertidaksamaan pecahan ini berbentuk hampir sama dengan pecahan pada bilangan real. Bentuk umumnya juga masih sama dengan pertidaksamaan sebelumnya yang terdiri dari: kurang dari (<), kurang dari sama dengan (≤), lebih dari (>) dan lebih dari sama dengan (≥).
Bentuk baku dari pertidaksamaan pecahan yaitu :
Berikut ini adalah tahapan dalam penyelesaian pertidaksamaan pecahan, diantaranya yaitu:
1). Ruas kanan dijadikan nol
2). Samakan penyebut di ruas kiri
3). Faktorkan pembilang dan penyebut (jika bisa)
4). Cari nilai-nilai variabel yang menyebabkan pembilang dan penyebutnya sama dengan nol (harga nol untuk pembilang dan penyebut)
5). Gambar garis bilangan yang memuat semua nilai yang didapatkan pada langkah
• Apapun tanda pertidaksamaannya, harga nol untuk penyebut selalu digambar dengan titik putih (penyebut suatu pecahan tidak boleh sama dengan 0 agar pecahan tersebut mempunyai nilai).
• Tentukan tanda (+) atau (–) pada masing-masing interval.
Contoh :
5. Pertidaksamaan bentuk akar (Irrasional)
Pertidaksamaan bentuk akar adalah pertidaksamaan yang variabelnya terdapat dalam tanda akar.
Pertidaksamaan mempunyai bentuk baku yaitu :
Berikut ini adalah tahapan dalam penyelesaian pertidaksamaan pecahan, diantaranya yaitu:
1). Menguadratkan kedua ruas.
2). Pengecekan syarat akar, di mana kita akan memastikan apabila fungsi di dalam akar pangkat dua haruslah bernilai positif atau sama dengan nol begitu juga dengan konstanta di ruas lainnya.
3). Tentukan interval yang memenuhi penyelesaiannya, Tentukan tanda (+) atau (–) pada masing-masing interval
Apapun tanda pertidaksamaannya, harga nol untuk penyebut selalu digambar dengan titik putih (penyebut suatu pecahan tidak boleh sama dengan 0 agar pecahan tersebut mempunyai nilai).
Contoh :
6. Persamaan Nilai Mutlak
Persamaan Nilai Mutlak adalah suatu nilai mutlak dari sebuah bilangan yang dapat didefinisikan sebagai jarak bilangan tersebut terhadap titik 0 pada garis bilangan tanpa memperhatikan arahnya.
Nilai mutlak atau modulus adalah nilai suatu bilangan riil tanpa adanya tanda tambah (+) atau kurang (–).
Nilai Mutlak
Nilai mutlak adalah Bilangan real x, yang dinyatakan dengan Variabel yang berada di dalam tanda mutlak |x|.
Didefinisikan dengan :
Contoh :
Contoh soal tambahan :
1.
2.
DAFTAR INTERVAL :
Cara menentukan Garis bilangan :
1. Jika tanda pertidaksamaan ≥ atau ≤, maka harga nol ditandai dengan titik hitam •
2.Jika tanda pertidaksamaan > atau <, maka harga nol ditandai dengan titik putih °
• Tentukan tanda (+) atau (–) pada masing-masing interval di garis bilangan. Caranya adalah dengan memasukkan salah satu bilangan pada interval tersebut pada persamaan di ruas kiri.
Rabu, 24 Maret 2021
FUNGSI
Fungsi adalah relasi yang menghubungkan elemen himpunan pertama (domain) secara tunggal pada elemen himpunan yang lain (kodomain). Artinya fungsi tidak akan pernah memiliki dua pasangan yang terdiri dari elemen pertama yang sama. Penulisan fungsi dilambangkan dengan :
f : x -> y
Dibaca “ f adalah fungsi dari x ke y”. Anggota y yang menjadi pasangan x oleh f disebut bayangan x dan ditulis Y = f(x).
Istilah – Istilah Dalam Fungsi :
• Domain = daerah asal fungsi f (dilambangkan dengan Df)
• Kodomain = daerah kawan fungsi f (dilambangkan dengan Kf)
• Range = daerah hasil yang merupakan himpunan bagian dari kodomain. Range fungsi f (dilambangkan dengan Rf)
• Variabel = simbol yang melambangkan faktor tertentu
• Variabel bebas =tidak tergantung pada variabel lain
• Variabel terikat=tergantung pada variabel lain
• Koefisien = angka pembentuk fungsi yang terkait pada variabel dalam sebuah fungsi
• Konstanta = angka yang kadang-kadang menjadi pembentuk fungsi,
• tidak terikat pada variabel
A. Macam-macam fungsi
Secara umum, dapat dikatan fungsi terdiri dari fungsi aljabar, fungsi transenden, fungsi khusus :
1. Fungsi aljabar
a. Fungsi irasional
b. Fungsi rasional
1) Fungsi linier
2) Fungsi polinom
3). Fungsi kuadrat
4). Fungsi pecahan
5). Fungsi kubik
2. Fungsi Transeden
1). Fungsi eksponen
2). Fungsi logaritma
3). Fungsi trigonometri
3. Fungsi khusus
1). Fungsi konstan
2). Fungsi identitas
3). Fungsi modulus
4). Fungsi genap dan ganjil
5). Fungsi tangga
6).Fungsi banyak persamaan
Berikut beberapa penjelasannya :
dengan:
· variabel x disebut
· variabel y atau f (x) disebut variabel terikat.
· Melukis Grafik Fungsi Linier :
Nilai a (koefisien dari x2 dapat memberi gambaran
grafik fungsi kuadrat tersebut terbuka ke atas atau ke bawah. Karakteristik
grafik berdasarkan nilai a:
·
Jika a > 0 maka grafik
akan terbuka ke atas.
·
Jika a < 0 maka grafik
akan terbuka ke bawah.
Gambaran umum Grafik fungsi kuadrat jika
dilihat dari nilai a dan D
1.
Menentukan
titik potong dengan sumbu x dan sumbu y (jika mudah ditentukan)
2. 1. Menentukan
asimtot tegak, asimtot datar dan asimtot miring
3. 2. Menetukan
interval dimana fungsi bernilai positif
4. 3. Menetukan
titik ekstrim
5. 4. Menentukan
titik bantu
6. 5. Melukis
sketsa grafik
Terdapat
3 asimtot :
1.
Asimtot
tegak diproleh penyebutnya 0
2.
Asimtot
datar diproleh jika x menuju tak hingga
3. Asimtot miring diproleh hanya untuk jenis fungsi rasional yang pembilangnya mempunyai derajat yang lebih tinggi dari pada penyebutnya
Contoh:
Gambarlah grafik fungsi y = 2log
x!
Langkah Pertama: ambil beberapa titik
absis (x) secara acak atau sembarang, sebagai masukan pilih nilai yang
menghasilkan nilai logaritma yang bagus dengan cara menyesuaikan dengan nilai
basisnya.
Ambil sembarang titik absis: misalnya kita
akan mengambil :
x = 1/4, 1/2, 1,4, dan 8
Langkah Kedua: tentukan nilai ordinat (y)
dari fungsi logaritma yang diberikan dan sekaligus menentukan titik
koordinatnya .
Langkah Ketiga: tentukan letak titik
koordinat yang diperoleh dalam bidang kartesius.
Langkah Keempat: hubungkan titik-titik yang diperoleh sehingga membentuk kurva mulus.
Kelima titik koordinat yang diperoleh
adalah dan (8,3). Letak kelima titik koordinat diberikan seperti gambar
berikut.
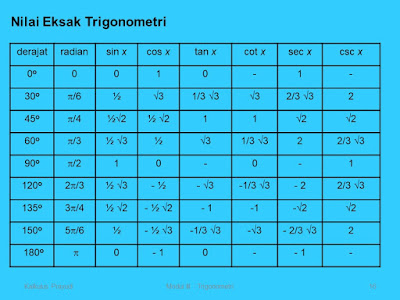
Nilai perbandingan trigonometri
sudut-sudut istimewa berperan penting dalam melukiskan bentuk grafiknya. Inilah
tabel perbandingan trigonometri untuk sudut istimewa.
1. Melukis grafik fungsi sinus menggunakan
tabel
Adapun langkah-langkahnya adalah sebagai berikut.
a. Gunakan nilai perbandingan trigonometri
untuk sudut istimewa dengan sudut relasi sebagai x.
b. Melengkapi nilai pada tabel, lalu tulis
pasangan koordinat titik-titiknya dalam radian atau derajat.
c. Lukis titik tersebut dalam koordinat
kartesius yang sesuai.
d. Lukis kurva melalui titik-titiknya.
Melukis grafik fungsi kosinus menggunakan
tabel
Sama seperti grafik fungsi sinus, untuk
kosinus kamu bisa menentukan terlebih dahulu nilai kosinus sudut-sudut
istimewanya.
>LIMIT
FUNGSI
Limit suatu fungsi
merupakan salah satu konsep mendasar dalam kalkulus dan analisis, tentang
kelakuan suatu fungsi mendekati titik masukan tertentu. Suatu fungsi memetakan
keluaran f(x) untuk setiap masukan x. Fungsi tersebut memiliki limit L pada
titik masukan p bila f(x) "dekat" pada L ketika x dekat pada p.
1). Limit Fungsi
f(x) untuk x => a, a ≠ 0.
Perhitungan
limit fungsi f(x) untuk x --> a, a ≠ 0 atau ditulis,
dapat dilakukan melalui tiga cara, yaitu substitusi langsung, pemfaktoran, dan
rasionalisasi bentuk akar.
Jika dengan cara substitusi langsung dihasilkan bentuk tak tentu.
maka perhingga limit dilakukan dengan cara pemfaktoran atau
rasionalisasi bentuk akar.
2).
Limit Fungsi F(x) untuk x => 0
Perhitungan limit fungsi f(x) untuk x → 0 atau di
tulis :
Pada prinsipnya sama seperti perhitungan pada :
3). Limit Fungsi f(x) → ~
Perhitungan
limit fungsi yang berbentuk :
Jika disubstitusikan langsung menghasilkan bentuk tak tentu.
Sehingga perhitungannya dilakukan dengan cara membagi pembilang
f(x) dan penyebut f(x) dan penyebut g(x) dengan xn, yang mana n adalah
pangkat tertinggi dari penyebut f(x). Perhitungan limit fungsi
yang berbentuk.
Teorema fungsi :
Sifat Limit Fungsi
Jika n adalah bilangan bulat positif, k konstanta, f dan g ialah fungsi-fungsi yang memiliki limit di c,
maka berlaku teorema-teorema berikut.
2. Limit
Fungsi Trigonometri
Limit fungsi
trigonometri memiliki definisi sebagai nilai terdekat suatu sudut dalam fungsi
trigonometri. Perhitungan ini dapat disubstitusikan layaknya limit fungsi
aljabar, tapi dengan fungsi trigonometri yang harus diubah terlebih dahulu.
Rumus-rumus limit fungsi trigonometri yang lain, yaitu :
1.
Teorema
L'Hospital
Dalil L'Hospital, kita sanggup menuntaskan limit dukungan fungsi f(x)⁄g(x) yang tidak terdefenisi dengan memakai dukungan turunan fungsi f(x) dan g(x). melaluiataubersamaini kata lain, jikalau f(x) = g(x) = 0 atau tidak terhingga, maka limit dari dukungan fungsi tersebut sanggup diselesaikan dengan limit hasil bagi turunannya.
Bentuk umum :
Jika, menghasilkan bentuk tak tentu (0/0),
Jika masih menghasilkan bentuk (0/0), maka
nilai dapat ditentukan dari turunan kedua, yaitu :
Rabu, 07 April 2021
LIMIT FUNGSI ALJABAR
A. Pengertian Limit Fungsi Aljabar
Limit dapat adalah suatu batas, sesuatu yang dekat namun tidak dapat
dicapai. Dalam bahasa matematika, keadaan ini dapat disebut limit. Suatu fungsi
biasanya tidak terdefinisi pada titik-titik tertentu, walaupun suatu fungsi
seringkali tidak terdefinisi untuk titik tertentu, namun masih dapat dicari
tahu berapa nilai yang didekati oleh fungsi tersebut apabila titik tertentu
semakin didekati yaitu dengan limit.
Dalam bahasa matematika, limit dituliskan dengan:
B.
Sifat-sifat Limit Fungsi Aljabar
Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku.
C.
Menentukan Nilai Limit Fungsi Aljabar
Ada 2 bentuk dalam menentukan limit fungsi aljabar
yaitu:
Bentuk
pertama
Bentuk
kedua
Ada beberapa metode atau cara penyelesaian untuk
limit aljabar, diantaranya yaitu :
·
Metode
subsitusi
·
Metode
pemfaktoran
·
Metode
memagi dengan pengkat tertinggi penyebut
·
Metode
mengalikan dengan faktor sekawan
Dalam hubungannya dengan bentuk limit yang pertama
ada beberapa metode dalam menentukan nilai limit fungsi aljabar yaitu dengan
cara substitusi dan cara pemfaktoran.
1.
Cara Substitusi
Cara substitusi ini langkahnya dengan mengganti peubah yang mendekati nilai tertentu dengan fungsi aljabarnya.
2.
Cara Pemfaktoran
Cara pemfaktoran digunakan apabila cara substitusi menghasilkan nilai limit yang tidak terdefinisikan seperti pada contoh berikut:
Cara pemfaktoran dilakukan dengan langkah menentukan
faktor persekutuan antara pembilang dan penyebuntya. Berikut beberapa contoh
untuk dipahami.
Contoh :
Tentukan nilai
limit fungsi aljabar dari
Jadi, nilai dari limit fungsi
aljabar tersebut,
Dalam hubungannya dengan bentuk limit yang kedua ada
beberapa cara dalam menentukan nilai limit fungsi aljabar yaitu metode membagi
dengan pangkat tertinggi penyebut dan metode mengalikan dengan faktor sekawan.
1.
Metode membagi dengan pangkat tertinggi penyebut
Contoh :
Tentukan nilai
limit fungsi aljabar dari
Besar pangkat pembilang dan penyebut dalam soal ini adalah 2, maka :
Jadi, nilai dari limit fungsi
aljabar tersebut,
2.
Metode mengalikan dengan faktor sekawan
Contoh
soal:
Tentukan nilai limit dari
Pertama yang perlu dilakukan untuk menentukan nilai
suatu limit yaitu dengan mensubtitusikan x=c ke f(x), sehingga dalam kasus ini
substitusikan
x=4 ke
LIMIT FUNGSI BILANGAN EULER (e)
& LIMIT FUNGSI TRIGONOMETRI
Bilangan Euler
Bilangan Euler (Euler’s Number) atau bilangan e
merupakan bilangan euler adalah
salah satu konstanta matematis berupa bilanan irasional dengan nilai 2,7182…..
yang di namai dari matematikawan Leonhard
Euler. Nilai
tersebut merupakan pendekatan dari aplikasi konsep limit berikut. Terdapat teorema limit bilangan euler. Teorema ini
sangat penting dalam menyelesaikan soal soal hitungan limit yang berkaitan
dengan bilangan euler.
Barisan bilangan dapat dianggap sebagai
fungsi dengan domain bilangan asli. Misalkan diberikan fungsi dengan n bilangan
asli.
Rumus fungsi tersebut dapat dikembangkan dengan menerapkan Ekspansi Newton,
yaitu :
Untuk n→∞, ditulis
Teorema 1 : Limit euler
Contoh :
Limit
fungsi trigonometri
Trigonometri merupakan cabang dari ilmu matematika
yang mempelajari hubungan antara panjang dan sudut segitiga, biasanya digunakan
dalam membuat desain bangunan, pembuatan jembatan, dan pada bidang astronomi.
Sedangkan
limit trigonometri merupakan nilai paling dekat dari suatu sudut.
Istilah-istilah yang ada dalam trigonometri yaitu sinus (sin), cosinus (cos),
tangen (tan), secan (sec), cosecan (csc), dan cotangent (ctg).
Rumus dasar limit
trigonometri :
Cara yang bisa digunakan untuk menentukan nilai limit suatu fungsi
trigonometri adalah sebagai beirikut :
- Metode Numerik
- Subtitusi
- Pemfaktoran
- Kali Sekawan
- Menggunakan Turunan
Macam – Macam Trigonometri
A. Macam – macam trigonometri
- Sinus ( sin )
- Tangen ( tan )
- Cosinus ( cos )
- Cotongen ( cot )
- Secan ( sec )
- Cosecan ( Csc )
B. Rumus kebalikan dalam
trigonometri
- sin∝ = 1/csc∝
- cos∝ = 1/sec∝
- tan∝ = 1/cot∝
- tan∝ = sin∝/cos∝
- cot∝=cos∝/sin∝
C. Identitas Trigonometri dalam
trigonometri
Sin2∝ + cos2∝ =1
1+cot2∝=csc2∝
Tan2∝+1=sec2∝
D. Rumus Jumlah dan Selisih
dalam trigonometri
E. Rumus Perkalian dalam
trigonometri
F. Rumus sudut rangkap dalam
trigonometri
Limit
fungsi trigonometri x mendekati suatu bilangan
Untuk dapat menentukan berapa nilai limit fungsi trigonometri untuk
x mendekati sebuah bilang c sebenarnya bisa dilakukan dengan mudah. Caranya
adalah dengan melakukan subsitusi nilai c pada fungsi trigonometri. Berikut ini
adalah persamaan rumus limit fungsi trigonometri:
Untuk lebih jelasnya kami akan memberikan contoh soal penggunaan
rumus limit fungsi trigonometri untuk x mendekati suatu bilangan.
Bentuk di dalam matematika ada 3 macam, yaitu :
1.
Bentuk terdefinisi (tertentu) yaitu bentuk yang nilainya ada dan
tertentu.
2.
Bentuk tak
terdefinisi yaitu bentuk
yang tidak mempunyai nilai.
3.
Bentuk tak
tentu yaitu bentuk
yang nilainya sembarang.
Limit Fungsi Trigonometri Untuk x mendekati 0 (teorema 1)
Limit Fungsi Trigonometri hanya berlaku pada saat x → c, Ɐc ∈ R (Teorema 2)
Contoh :
1.
2.
3.
4.
KONTINUITAS
Menurut kamus besar
bahasa Indonesia (KBBI), arti kata kontinu adalah
berkesinambungan; berkelanjutan; dan terus menerus. Jadi fungsi f dikatakan
kontinu di a jika tidak ada gangguan di grafik fungsi f di
titik x = a.
Lawan kata kontinuitas adalah diskontinuitas, fungsi f dikatakan tidak kontinu (diskontinu) di suatu titik a jika memenuhi salah satu dari tiga keaadaan tersebut.
Contoh :
BENTUK
LIMIT TAK TENTU-LIMIT FUNGSI
Ada beberapa macam limit tak tentu yaitu, sebagai berikut :
Berikut beberapa bentuk penyelesaian contoh limit tak tentu :
1. Bentuk Tak Tentu 0/0
Penyelesaian :
Contoh :
2. Bentuk Tak Tentu Tak hingga per Tak hingga
Penyelesaian :
Contoh :
3. Bentuk Tak Tentu 0. Tak hingga
Penyelesaian :
.
Contoh :
4. Bentuk Tak Tentu Tak hingga - Tak hingga
Penyelesaian :
Contoh :
5. Bentuk Tak Tentu 0^0
Penyelesaian :
Contoh
:
6. Limit Tak Tentu Tak hingga ^ 0
Penyelesaian :
Contoh :
7. Bentuk Tak Tentu 1 ^ Tak Hingga
Penyelesaian :
Contoh :
Rabu, 16 Juni 2021
TURUNAN
IMPLISIT
1.
Turunan Implisit
Fungsi implisit yaitu fungsi yang memuat dua variabel atau lebih. Variabel-variabel tersebutterdiri dari variabel bebas dan variabel tidak bebas. Biasanya variable-variabel tersebutdinyatakan dalam x dan y. Dimana variabel x dan y terletak didalam satu ruas sehingga tidak dapat dipisahkan menjadi ruas yang berbeda (baca : ruas kiri dan ruas kanan) sepertihalnya fungsi eksplisit. Fungsi Implisit adalah secara umumdapat ditulis sebagai f (x,y) = 0 , denganya sebagai fungsi dalam x . Fungsi ini dapat dinotasikan dengan y = f (x) yangdisebut fungsi eksplisit , yaitu antara variabel bebas dan variabel tak bebasnya di tulisdalam ruas yang berbeda.
Langkah-langkah untuk
menghitung turunan fungsi secara implisit adalah :
· a. Terapkan aturan rantai pada setiap suku
yang terlibat pada persamaan,
· b. Kumpulkanlah suku yang memuat turunan pada ruas kiri dan yang lain di ruas kanan, dan selesaikan persamaan turunan
Menurunkan fungsi implisit terhadap x dapat dilakukan dengan cara seperti berikut ini:
1. Turunkan
kedua ruas (ruas kanan dan ruas kiri) terhadap x.
2. Gunakan
aturan rantai
3.
Tentukan dy/dx
Contoh Soal :
Rabu, 30 Juni 2021
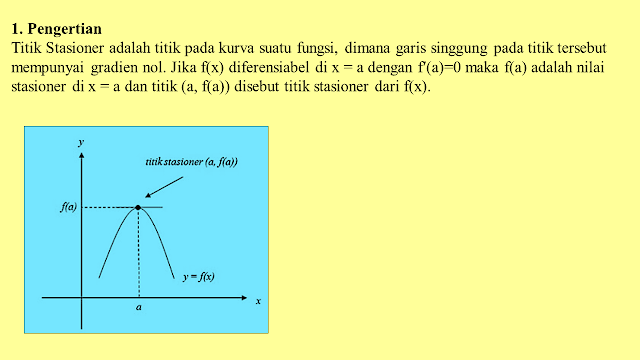
TITIK STASIONER DAN TITIK BELOK
TERIMAKASIH.